Haaland Equation Accuracy Comparison
haaland

Mastering the Haaland Equation in MATLAB

January 26, 2025 By Marquinhos

The Haaland equation is a crucial tool for engineers dealing with fluid flow, and understanding how to implement it in MATLAB can significantly streamline your calculations. This article provides a comprehensive guide to the Haaland Equation In Matlab, covering everything from its theoretical underpinnings to practical applications. haaland equation matlab We’ll explore how this powerful equation can help you determine the Darcy friction factor, a key parameter in fluid dynamics.

The Haaland equation provides an explicit approximation for the Darcy friction factor in turbulent pipe flow, a more efficient alternative to the implicit Colebrook-White equation. It allows for quicker and easier computation, especially beneficial within MATLAB scripts and functions. Knowing how to effectively utilize this equation in MATLAB unlocks a world of possibilities for fluid flow analysis and design.

Understanding the Haaland Equation

The Haaland equation is an explicit approximation of the Colebrook-White equation. It’s significantly easier to compute, making it a preferred choice for many engineering applications. The equation is defined as:

1/√f = -1.8log[(ε/D/3.7)^1.11 + 6.9/Re]

Where:

  • f represents the Darcy friction factor
  • ε denotes the pipe roughness
  • D signifies the pipe diameter
  • Re represents the Reynolds number

This equation provides a convenient way to estimate the friction factor without resorting to iterative methods required by the Colebrook-White equation.

Implementing the Haaland Equation in MATLAB

MATLAB’s powerful computational environment makes implementing the Haaland equation straightforward. Here’s a step-by-step guide:

  1. Define Variables: Assign values to the pipe roughness (epsilon), pipe diameter (D), and Reynolds number (Re). Ensure consistent units.

  2. Implement the Equation: Translate the Haaland equation into MATLAB code:

f = 1/(-1.8*log10((epsilon/D/3.7)^1.11 + 6.9/Re))^2;
  1. Display the Result: Use the disp function to show the calculated friction factor:
disp(['Friction factor (f): ', num2str(f)]);

Why Use the Haaland Equation?

Why choose the Haaland equation over others? Its explicit nature allows for direct calculation of the friction factor, eliminating the need for iterative solvers. This makes it particularly useful in MATLAB, where computational efficiency is often paramount. The haaland equation for friction factor is a quick and reliable method for determining this important parameter.

What are the limitations of the Haaland Equation?

While the Haaland equation offers advantages, it’s essential to be aware of its limitations. As an approximation, it may not be as accurate as the Colebrook-White equation, particularly in certain flow regimes. However, for most engineering applications, its accuracy is sufficient.

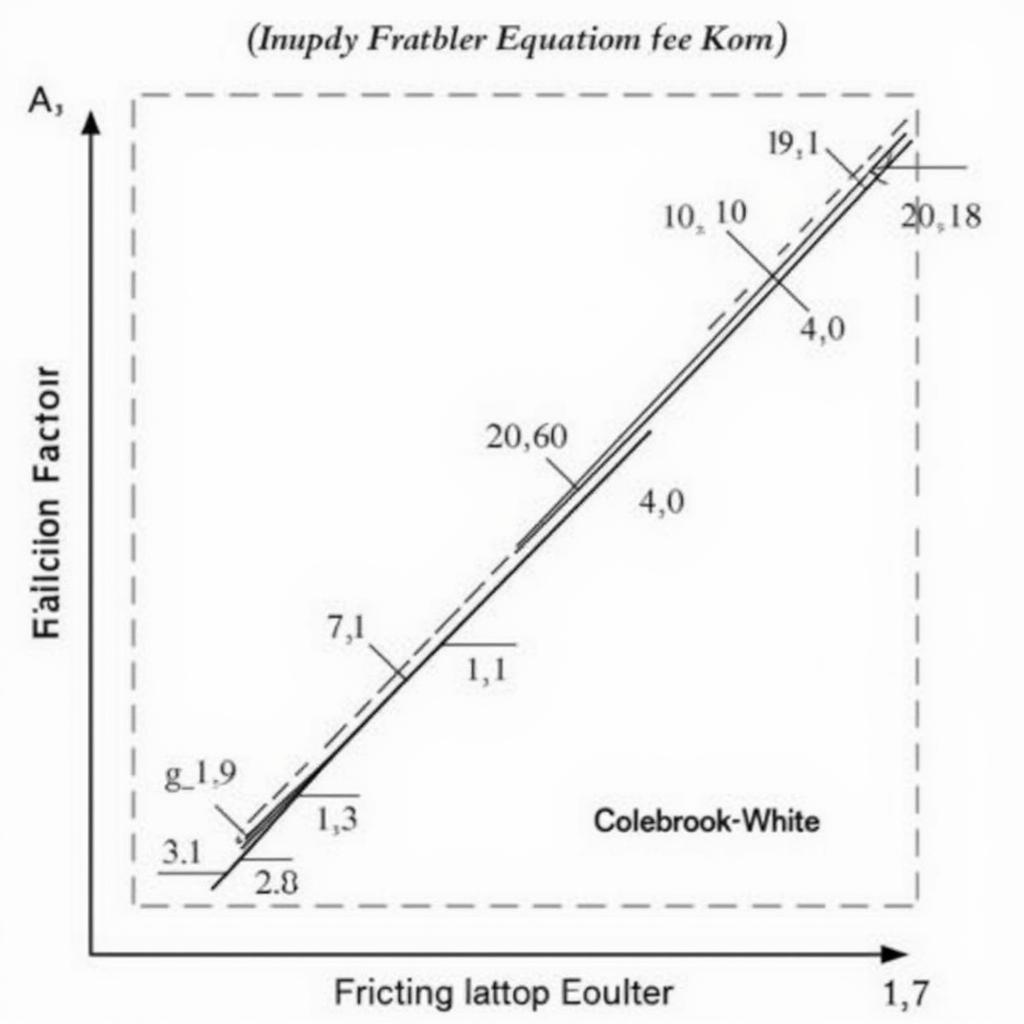Haaland Equation Accuracy ComparisonHaaland Equation Accuracy Comparison

Conclusion

The Haaland equation provides a powerful and efficient method for calculating the Darcy friction factor in MATLAB. Its explicit nature simplifies calculations and its accuracy is generally sufficient for practical engineering purposes. Mastering this equation in MATLAB will enhance your ability to analyze and design fluid flow systems. Remember to consider its limitations and choose the most appropriate method for your specific application. Use the haaland equation matlab effectively for your fluid dynamics projects.

FAQ

  1. What is the main advantage of the Haaland equation? Its explicit form allows for direct calculation of the friction factor.

  2. Is the Haaland equation always accurate? It’s an approximation, so while generally accurate, it might deviate slightly from the Colebrook-White equation in some cases.

  3. What is the Darcy friction factor? A dimensionless parameter representing the frictional losses in pipe flow.

  4. What is the Reynolds number? A dimensionless quantity that helps determine the flow regime (laminar or turbulent).

  5. How can I learn more about the haaland vector? Visit our dedicated page for comprehensive information.

  6. Where can I find examples of haaland 11 goals? Explore our website for highlights and detailed statistics.

For assistance, contact us at Phone: 0396443476, Email: [email protected] or visit us at 23 Tháng 3, Đắk Nia, Gia Nghĩa, Đắk Nông, Việt Nam. Our customer support team is available 24/7.